Gottfried Leibniz: Metaphysics

Source: https://iep.utm.edu/leib-met/

The German rationalist philosopher, Gottfried Wilhelm Leibniz (1646-1716), is one of the great renaissance men of Western thought. He has made significant contributions in several fields spanning the intellectual landscape, including mathematics, physics, logic, ethics, and theology. Unlike many of his contemporaries of the modern period, Leibniz does not have a canonical work that stands as his single, comprehensive piece of philosophy. Instead, in order to understand Leibniz’s entire philosophical system, one must piece it together from his various essays, books, and correspondences. As a result, there are several ways to explicate Leibniz’s philosophy. This article begins with his theory of truth, according to which the nature of truth consists in the connection or inclusion of a predicate in a subject.

Together with several apparently self-evident principles (such as the principle of sufficient reason, the law of contradiction, and the identity of indiscernibles), Leibniz uses his predicate-in-subject theory of truth to develop a remarkable philosophical system that provides an intricate and thorough account of reality. Ultimately, Leibniz’s universe contains only God and non-composite, immaterial, soul-like entities called “monads.” Strictly speaking, space, time, causation, material objects, among other things, are all illusions (at least as normally conceived). However, these illusions are well-founded on and explained by the true nature of the universe at its fundamental level. For example, Leibniz argues that things seem to cause one another because God ordained a pre-established harmony among everything in the universe. Furthermore, as consequences of his metaphysics, Leibniz proposes solutions to several deep philosophical problems, such as the problem of free will, the problem of evil, and the nature of space and time. One thus finds Leibniz developing intriguing arguments for several philosophical positions—including theism, compatibilism, and idealism.

This article is predominately concerned with this broad view of Leibniz’s philosophical system and does not deal with Leibniz’s work on, for example, aesthetics, political philosophy, or (except incidentally) physics. Leibniz’s “mature metaphysical career” spanned over thirty years. During this period, it would be surprising if some of his basic ideas did not change, but, remarkably, the broad outline of his philosophy does remain constant.

1. Life

Gottfried Wilhelm Leibniz was born in Leipzig, Germany, on July 1, 1646. He was the son of a professor of moral philosophy. After university study in Leipzig and elsewhere, it would have been natural for him to go into academia. Instead, he began a life of professional service to noblemen, primarily the dukes of Hanover (Georg Ludwig became George I of England in 1714, two years before Leibniz’s death). His professional duties were various, such as official historian and legal advisor. Above all, he was required to travel widely, meeting many of the foremost intellectuals in Europe—of particularly formative importance were the astronomer, mathematician, and physicist Huygens, and the philosopher Spinoza.

Leibniz was one of the great polymaths of the modern world. Moreover, a list of his significant contributions is almost as long as the list of his activities. As an engineer, he worked on calculating machines, clocks, and even mining machinery. As a librarian, he more or less invented the modern idea of cataloguing. As a mathematician, he not only produced ground-breaking work in what is now called topology, but came up with the calculus independently of (though a few years later than) Newton, and his notation has become the standard. In logic, he worked on binary systems, among numerous other areas. As a physicist, he made advances in mechanics, specifically the theory of momentum. He also made contributions to linguistics, history, aesthetics, and political theory.

Leibniz’s curiosity and genius ranged widely, but one of the most constant of his concerns was to bring about reconciliation by emphasizing the truths on each side of even the most seemingly contradictory positions. Throughout his life, he hoped that his work on philosophy, as well as his work as a diplomat, would form the basis of a theology capable of reuniting the Church, which had been divided since the Reformation in the 16th Century. Similarly, he was willing to engage with, and borrow ideas from, the materialists as well as the Cartesians, the Aristotelians as well as the most modern scientists. It is quite ironic, then, that he was a partial cause of a dispute between British and Continental mathematicians concerning who was first to develop the calculus (and who might have plagiarized who), a dispute which slowed the advance of mathematics in Europe for over a century.

However, the great variety of Leibniz’s work meant that he completed few of his ambitious projects. For present purposes, this means above all that Leibniz’s rich and complex philosophy has to be gathered primarily from a large set of quite short manuscripts, many fragmentary and unpublished, as well has his various correspondences. (The last section of this article provides bibliographical details of several editions of Leibniz’s work.) As a result, a major controversy in Leibniz scholarship is the question of where to begin. Insofar as Leibniz is a logician, it is tempting to begin with his conception of truth (and, indeed, this will be the starting point of this article). But insofar as Leibniz is a metaphysician, it is equally tempting to begin with his account of the nature of reality, in particular his notion of substance as monads. Less common, but perhaps equally likely, starting points might reside in Leibniz the mathematician, the theologian, or the physicist. These controversies, however, already contain a lesson: to an important degree it doesn’t matter. So integrated were his various philosophical interests—so tightly laced together into a system — that one ought to be able to begin anywhere and reconstruct the whole. Or at least Leibniz evidently thought so, since often he uses an idea from one part of his philosophy to concisely prove something in an apparently quite distant philosophical region. However, due to this systematic nature of his philosophy, in which every idea seems to rely upon others, engaging Leibniz’s ideas often proves to be challenging.

2. The Idea of Truth

According to Leibniz, a conception of truth has important consequences for a conception of reality and how it is to be understood at its most profound level. Intuitively, a proposition is true when its content is adequate to the situation in the world to which it refers. For example, “the sky is gray” is true if and only if the thing out there in the world called “the sky” is actually the color called “gray” at the time the proposition is stated. This, however, raises issues about the relationship of language to the world and what “adequacy” consists in.

Leibniz claims that one can bypass problems with the intuitive notion of truth, at least for the moment. Truth, according to Leibniz, is simply a proposition in which the predicate is contained in the subject. The predicate is what is asserted; the subject is what the assertion is about. All true propositions, then, can be expressed by the following general form: “subject is predicate.” This is not, by any means, an idea unique to Leibniz. What is unique, however, is the single-mindedness with which he pursues the consequences of such an idea of truth. (See, for example, “Correspondence with Arnauld,” 14 July 1686.)

This notion of truth seems straight-forward enough for what are commonly called analytic propositions, such as “Blue is a color,” which has more to do with the definition of blue than it does with the world. The notion of color is part of the notion of blue. Similarly, in the basic logical truth “A is A,” the predicate is not just contained in the subject, it is the subject. But, Leibniz states that this “being contained” is implicitly or virtually the case with other truths (see “Primary Truths” and “The Nature of Truth”). Take, for example, the statement “Peter is ill.” Intuitively, this proposition is true only if it refers to a real world in which Peter is, in fact, ill. Leibniz, however, analyzes this as follows: if one knew everything there is to know about Peter, that is, if one had a complete concept of Peter, one would also know (among many other things) that he is ill at the moment. Therefore, the statement “Peter is ill” is true not primarily because of some reference to the world, but in the first instance because someone has the concept of Peter, which is the subject of the proposition, and that concept contains (as a predicate) his being ill. Of course, it may be the case that one happens to know that Peter was ill because one refers to the world (perhaps sees him cough repeatedly). But the fact that one finds out about Peter in this way does not make the statement that “Peter is ill” true and thus a piece of knowledge because of that reference. One must distinguish the concept of truth from pragmatic or methodological issues of how one happens to find out about that truth, or what one can do with the truth. The latter, according to Leibniz, are completely irrelevant to the question “What is truth?” in itself.

Leibniz also claims that a statement is true for all time—that is, whenever the statement is made. So, for example, the statement “Peter is ill (on January 1st, 1999)” was true in the year 1998 (even though no one knew it yet) as well as in the year 2000 (even though everyone may have forgotten about the illness by then). It was also true a million years ago, and will be true a million years from now, although it is very unlikely that anyone will actually know this truth at those times.

Leibniz’s own example is of Julius Caesar. He writes:

However, there are several ideas Leibniz introduces in this passage that require further investigation. What is meant by “completing the whole demonstration,” by something having a “foundation,” or by “a reason can be found?”

3. Sufficient Reason

As previously stated, for any proposition, truth is defined by Leibniz in the same way: the predicate is contained in the subject. It only takes a little thought to realize that for any one subject (like Peter or Caesar), the number of predicates which are true of it will be infinite (or at least very large), for they must include every last thing Peter or Caesar did or will do, as well as everything that did or will ever happen to them. But now it is natural to ask: Why do all these predicates come together in the one subject? It could be that the predicates are a quite arbitrary or random collection — although Leibniz does not believe this, and it is certainly not intuitive. Rather, one predicate or set of predicates explains another. For example, Peter’s coming into contact with a virus explains his illness. Or, Caesar’s ambition and boldness explains why he decided to cross the Rubicon. So, many (at least) of the predicates that are true of a subject “hang together” as a network of explanations.

Leibniz goes further still by claiming that for every predicate that is true of a subject, there must be a set of other true predicates which constitute a sufficient reason for its being true. This he calls the principle of sufficient reason — that there must be a sufficient reason for why things are as they are and not otherwise. This is why he uses words like “foundation” and “reason” in the quotation above. Unless this were true, Leibniz argues, the universe would not make any sense, and science and philosophy both would be impossible (see, for example, New Essays on Human Understanding, preface, p. 66). Moreover, it would be impossible to account for a basic notion like identity unless there was a sufficient reason why Caesar, for example, with his particular properties at a given time, is identical with the Caesar who existed a week prior with such different properties (see “Remarks on Arnauld’s Letter,” May 1686).

The principle of sufficient reason also accounts for why Leibniz uses the phrase “completing the whole demonstration” in the above quote. If the complete concept of the subject (that is, all of its true predicates) together constitutes a complete network of explanation, then these explanations can be followed forward and backward, so to speak, at least in principle. That is, working forward, one coulddeduce that Caesar will cross the Rubicon from a all the predicates that have been true of him; or, working backward, one can deduce from all those predicates true of Caesar at his death the reasons why he won the battle of Pharsalus. The “whole demonstration,” then, is the revelation of the logical structure of the network of explanations that make Caesar who he is.

However, this is clearly not something the average person can do. Human minds are not subtle and capacious enough for a task which may be infinite. Still, in a more limited way, one can certainly talk about personalities, characters, and causes or reasons for things. The quotation from Leibniz given above continues:

These qualifications are quite important for Leibniz. It was often suggested by Leibniz’s contemporaries (and is still being suggested) that his idea of the sufficient reason of all the predicates of a subject meant that everything true of a subject is necessarily true. This might entail that Caesar did not choose to cross the Rubicon, but that he was acting in a determined manner, like a machine. In other words, Leibniz seems to be denying any sort of free will. The free will problem will be discussed in more detail below, but for the moment, a few observations can be made.

First, Leibniz claims that Caesar’s crossing of the Rubicon is not necessary in the sense that “A is A” is necessary. Because while “A is not A” is a contradiction, Caesar’s deciding not to cross the Rubicon does not imply a contradiction. To be sure, history would have been different—even Caesar would have been different—but there is no contradiction in that strong sense. Caesar’s properties are not logically necessary.

Second, any truth about Caesar–indeed, the whole complete concept of Caesar–is not “necessary in itself.” Caesar is Caesar, but nothing about Caesar in himself proves that Caesar has to be. By contrast, “A is A” doesn’t need any other explanation for its truth. So, while every property of Caesar is explained by some other property of Caesar, no property explains why it is true that Caesar existed. Caesar is not a necessary being.

What the precise details are of Leibniz’s account of free will remain a strenuously debated issue in Leibniz scholarship (especially what the exact nature is of these distinctions, whether he is justified in making them, and even if justified whether they yield the results he claims in the area of free will). More detail will be added to this account below, but the existence of this debate should be kept in mind throughout.

4. Substance, Briefly

At this point, it is useful to turn from a conception of truth to a conception of substance. Leibniz’s philosophy of substance will be explicated in more detail in section 8 (Substance as Monad). For the moment, simply observe that for humans (though not for God), complete concepts are always concepts of existing substances–that is, of really existing things. Leibniz writes:

To be the individual substance, Caesar, then, is to be such as to have a notion which includes everything that can truthfully be predicated of the subject Caesar. Thus, one might say that, for Leibniz, a substance is a complete concept made real, and a complete concept is a real substance expressed or “perceived” in thought. Moreover, just as for any one predicate, the complete concept contains other predicates which explain that predicate, for any given property of a substance, the complete individual substance will itself be the explanation for that property. Caesar chose to cross the Rubicon for many complex reasons, but they all boil down to this: that was the kind of individual Caesar was.

Leibniz has much more to say about substance, but he claims that it all follows from this insight. However, the exact relationship Leibniz intended between the logical idea of a complete concept and the metaphysical idea of a substance is still debated in Leibniz scholarship.

5. Necessary Being

The complete concept of Caesar, according to Leibniz, cannot explain itself in its entirety. Expressed ontologically, this means that Caesar himself provides no explanation of why Caesar should have existed at all–Caesar is a contingent being. “Contingent” here simply means something that could have been otherwise; in the case of Caesar as a being, then, it means something that could have not existed at all. The principle of sufficient reason must not only apply to each predicate in the complete concept of a subject, but also it must apply to the concept itself in its entirety as the concept of an existing thing. Thus, there must be a sufficient reason for why this particular substance, Caesar, exists, rather than some other substance, or nothing at all.

What, then, sufficiently explains a contingent being such as Caesar? Possibly other substances, such as his parents, and they in turn are explained by still others? But the entire course of the universe, the total aggregate of substances across space and time, are one and all contingent. There are other possible things, to be sure; but there are also other possible universes that could have existed but did not. The totality of contingent things themselves do not sufficiently explain themselves. Here again, the principle of sufficient reason applies. There must be, Leibniz insists, something beyond the totality of contingent things which explains them, something which is itself necessary and therefore requires no explanation other than itself. (Note, however, that this does not assume an origin or beginning in any sense. Even if time stretched infinitely into the past, there would still be no explanation for the total course of things.)

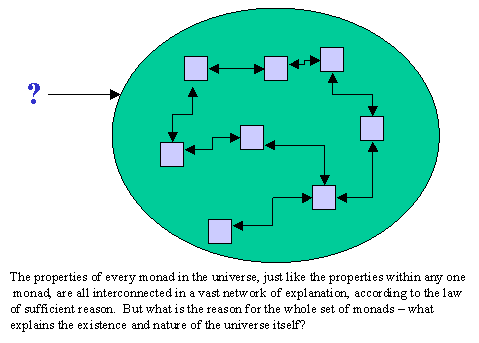
God, according to Leibniz, is the necessary being which constitutes the sufficient explanation of the totality of contingent things–why the universe is this way rather than any other. Thus far, God’s necessity is the only thing mentioned about such a being (there is not much religious or theological about this initially bare metaphysical concept). God as a being may be necessary, but if the contingent universe were simply a random or arbitrary act of God, then God would not constitute the required explanation of all things. In other words, God must not only be necessary, but also the source of the intelligibility of all things. It must be possible, therefore, to inquire into the reasons God had for authorizing or allowing this, rather than any other, universe to be the one that actually exists. And if God is to be the explanation of the intelligibility of the universe, then God must have access to that intelligibility, such that God could be said to know what it is that is being allowed to exist–that is, God must have the ability to grasp complete concepts, and to see at once the “whole demonstration” discussed above. God so far is therefore (i) a necessary being, (ii) the explanation of the universe, and (iii) the infinite intelligence.

Here Leibniz famously brings in the notion of perfection (see, for example, “A Specimen of Discoveries”). One has to try to imagine God, outside of time, contemplating the infinite universe that “he” is going to, not create, but allow to be actual and sustain in existence. In the mind of God are an infinite number of infinitely complex and complete concepts, all considered as possibly existent substances, none having any particular “right” to exist. There is just one constraint on this decision: it must not violate the other basic principle of Leibniz’s, the law of non-contradiction (also known as “the law of contradiction”). In other words, each substance may individually be possible, but they must all be possible together–the universe forming a vast, consistent, non-contradictory system. For example, God could not create a universe in which there are both more sheep than cows and more cows than sheep. God could choose a universe in which there is the greatest possible quantity of pizza, or in which everything is purple, and so on. However, according to Leibniz, God chooses the universe that is the most perfect. This principle of perfection is not surprising since it is most consummate with the idea of God as an infinite being; to choose any other less perfect universe would be to choose a lesser universe. Thus, according to Leibniz, the actual world is the best of all possible worlds. (This claim, and its apparent implications, were very effectively and famously satirized by Voltaire in his Candide. Note also that Leibniz is often taken as an ancestor of modern possible worlds semantics; however, it is undeniable that at least the context and purpose of Leibniz’s notion of a possible universe was quite different.) Leibniz explores the theological consequences of this at, for example, the end of Discourse on Metaphysics. (There may be a difficult theological implication here: must God be thought of as constrained, first by the concept of perfection, and then by the systemic nature of his creation? Leibniz attempts, for example, in the “Correspondence with Arnauld” to escape this conclusion.)

To try to understand further this notion of perfection, Leibniz explores several concepts in various writings: notions of the best, the beautiful, the simply compossible, greatest variety or the greatest quantity of essence. The last of these is the explanation he continually comes back to: perfection simply means the greatest quantity of essence, which is to say the greatest richness and variety in each substance, compatible with the least number of basic laws, so as to exhibit an intelligible order that is “distinctly thinkable” in the variety (see “A Resume of Metaphysics;” there is a relationship to the Medieval, and particularly Augustine, notion of plenitude). Leibniz seems to understand this principle as simply self-evident. It certainly seems to be a big jump to the aesthetic, moral, and wise God from the ontological conception of God deduced above. However, Leibniz may have a point in arguing that it would be absurd in some sense for an infinite being to choose anything other than an infinitely rich and thus perfect universe. He also finds this aesthetic observed throughout nature: natural forms tend towards a maximum of variety compatible with orderliness. Nevertheless, contemporary philosophers generally find Leibniz’s conclusion here to not strictly follow from the previous considerations.

For Leibniz, this forms a proof for the existence of God (see Monadology §§37-39 and “A Specimen of Discoveries”). In fact, it is a version of the third of the cosmological arguments given by St. Thomas Aquinas, and subject to many of the same difficulties. One might, for example, object in a Kantian vein that the concept of explanation, rightly demanded of all individual contingent beings, is applied beyond its proper sphere in demanding an explanation of the totality of contingent beings. But Leibniz might well counter that this objection assumes a whole theory of the “proper spheres” of concepts.

6. Problems of Freedom, Sin, and Evil

a. Freedom and Sin

Leibniz’s conception of God, however, may seem to cause more problems than it solves. For example, if the complete concept of any being, such as a human being, is known for all time, and was chosen by God for existence, then is such a being free? It seems that what one means by “freedom” is that the outcome is not predictable, as opposed to, for example, the way in which the operation of a washing machine or the addition of two numbers is predictable. Further, what must one make of morality and sin? Why, for example, should God punish Adam and Eve for sinning when they seemed to have no free choice, since God knew in advance (predicted and, indeed, made it the case) that they were going to sin?

While Leibniz’s philosophical system demands a certain sense of determinism about the universe, he does not want to deny the existence of free will. Leibniz thus seeks to substantiate a form or compatibilism (that is, a view which takes determinism to be compatible with free will). In order to accomplish this, Leibniz distinguishes between several ways in which things might be determined in advance. Whatever is determined is clearly true. Truth, however, comes in several varieties. (Much of the following is taken from the set of distinctions Leibniz makes in “Necessary and Contingent Truths;” Leibniz makes similar but rarely identical sets of distinctions in a variety of texts.)

1. Truths of Essence

• These come in two varieties:
  1. Primary/original truth: the law of non-contradiction, for example.
  2. Eternal, metaphysical, or geometrical truths: the laws of arithmetic or geometry, for example, which Leibniz claims can be reduced by a finite process of argumentation and substitution of definitions to primary truth. These are valid in all possible universes.

2. Truths of Existence, of Fact, or of Hypothesis

• Here, arguably, Leibniz sees four varieties:
  1. Absolutely universal truths: those truths definitive of this universe as being the most perfect universe. Leibniz writes: “Indeed, I think that in this series of things there are certain propositions which are true with absolute universality, and which cannot be violated even by a miracle” (“Necessary and Contingent Truths”).
  2. Universal-physical truths: the laws of physics and other such efficient causes, for example; truths which hold universally of all substances in this, but not in all possible, universes, but which also could, in principle, be violated by a miracle, in accordance with overall divine providence.
  3. Individual metaphysical truths: truths about the properties of individual substances, where those properties follow from the complete concept–and thus are apparent to God, but do not follow any “subordinate universal laws.” Deduction of such truths is available to no being, no matter how perfect or perceptive, other than God.
  4. Hypothetical truths: only truths of essence can be necessary, absolutely and strictly speaking. All other truths, such as the actions of Caesar, are only “hypothetically” necessary–that is, only on the hypothesis that a universe exists as it is, with beings such as these in it (see Discourse on Metaphysics, §13 and “Correspondence with Arnauld,” April 12th, 1686).

A person’s actions are, therefore, not necessary by definition (regardless, at this point, of which type of “truth of existence” they fall under). Thus, the concept of an individual “inclines without necessitating” (see Discourse on Metaphysics, §30). Leibniz further writes:

By “indifference,” Leibniz means a physical indifference–that is to say, there is no universal-physical truth, as defined above, which governs human action. For Leibniz, this means that human action is further freed: the will has the power to suspend its action with respect to the physical sequence of efficient causes, but also even with respect to what would otherwise be seen as a decisive final cause. Leibniz states: “For they [free or intelligent substances] are not bound by any certain subordinate laws of the universe, but act as it were by a private miracle” (“Necessary and Contingent Truths”).

Minds, then, are different from mechanical causes. (As it will be shown below, Leibniz goes against the trend of 17th and 18th century thought by reintroducing the Aristotelian and Scholastic notion of a final cause and, indeed, substantial forms.) Although Leibniz occasionally uses the analogy of a machine to describe the soul, the kinds of forces and causes operative in the former are simply inapplicable to the latter. Thus, if by individual free choice one means an individual action that cannot be known in advance by even an infinitely subtle application of the laws of physics, chemistry, or biology, then humans have free choice in that sense as well.

Leibniz also offers the following additional arguments for his particular conception of human free will:

1. Freedom as “unpredictability” might be taken to mean freedom as an act uncaused. But this makes no sense, for free choice is not randomness. Caesar’s free act, for example, has a cause–namely, Caesar. Why should one complain when the individual concept of Caesar intrinsically determines what Caesar does? Isn’t Caesar free if he is the source of his action, and not anyone or anything else?
2. A necessary ignorance of the future is practically, perhaps even logically, equivalent to freedom. Again, grasping the full explanation of any predicate that lies in the complete concept is an infinite task. To help illustrate the distinction between contingent and necessary truths, Leibniz makes a famous analogy with the incommensurability of any whole number or fraction with a “surd” (for example, the square root of two, the value of which cannot be represented numerically by any finite series of numbers.) For finite human minds, that incommensurability is a positive fact, just like contingency–no matter that for God neither calculation is impossible, or even more difficult. Thus contingent truths can in principle be known from all time, but necessarily not by a human being (see, for example, “On Freedom”). Leibniz writes: “Instead of wondering about what you cannot know and what can tell you nothing, act according to your duty, which you do know” (Discourse on Metaphysics, §30). (It should be pointed out that this is somewhat more than an analogy, since it is closely related to the kinds of problems infinitesimal calculus was designed to deal with–and Leibniz takes the possibility of a calculus as having real metaphysical implications.)
3. A famous scholastic debate concerned the so-called “Sloth Syllogism.” If everything is fated, the argument goes, then whatever action one “does” will or will not happen whether or not one wills it, therefore one need not will anything at all. One can just be a sloth, and let the universe happen. Leibniz thinks this is absurd–indeed, immoral. The will of an individual matters. If John Doe is the kind of person who is a sloth, then (everything else being the same) the course of his life will indeed be quite different than if he is the kind of person (like Caesar) who takes events by the scruff of the neck.
4. What many philosophers mean by “contingent” is that an individual predicate “could have been different,” and everything else the same. For Leibniz, this is impossible. To change one predicate means to alter the whole complete concept, the substance, and with it the whole universe. Leibniz thus claims that philosophers of a more radical sense of freedom do not take seriously the extent to which the universe is an integrated network of explanations, and that this in turn has implications for the idea of contingency (see the discussion of Adam in Leibniz’s letter to Landgraf Ernst von Hessen-Rheinfels, April 12, 1686). Thus, contingent events, even one’s free acts, must be part of the perfection of the universe. Although, that does not mean that all contingent events are so in the same way.

According to Leibniz, any remaining objections to this idea of free will only result from a metaphysically incoherent idea of what freedom means. There is no question that Leibniz introduced a spirited and powerful position into the age-old philosophical debate concerning free will. Which position is “metaphysically incoherent,” however, remains under debate. (For more on the philosophical debate of free will, see “Free Will“.)

b. Problem of Evil

Leibniz’s approach to the classic problem of evil is similar. The problem of evil, for Leibniz, can be put in the following way: If God is supremely good, and the creator (or author) of the best possible universe, then why is there so much pain and sin in the world? Leibniz claims that this apparent paradox is not a real problem. Leibniz coined the term “theodicy” to refer to an attempt to reconcile God’s supremely benevolent and all-good nature with the evil in the world. Thus, Leibniz’s Theodicy is largely a proposed solution to the problem of evil. However, his thoughts on the issue are to be found spread over many texts. (For more on the problem of evil, see the entries “The Evidential Problem of Evil” and “The Logical Problem of Evil.”)

Here, very briefly, are three of Leibniz’s main replies to the problem of evil:

1. Human minds are only only aware of a small fraction of the universe. To judge it full of misery on this small fraction is presumptuous. Just as the true design–or, indeed, any design–of a painting is not visible from viewing a small corner of it, so the proper order of the universe exceeds one’s ability to judge it.
2. The best possible universe does not mean no evil, but that less overall evil is impossible.
3. Similarly to the previous argument, and in the best Neo-Platonist tradition, Leibniz claims that evil and sin are negations of positive reality. All created beings are limitations and imperfect; therefore evil and sin are necessary for created beings (see Discourse on Metaphysics, §30).

7. Space, Time, and Indiscernibles

a. Against the Absolute Theory

Between 1715 and 1716, at the request of Caroline, Princess of Wales, a series of long letters passed between Leibniz and the English physicist, theologian, and friend of Newton, Samuel Clarke. It is generally assumed that Newton had a hand in Clarke’s end of the correspondence. They were published in Germany and in England soon after the correspondence ceased and became one of the most widely read philosophical books of the 18th Century. Leibniz and Clarke had several topics of debate: the nature of God’s interaction with the created world, the nature of miracles, vacua, gravity, and the nature of space and time. Although Leibniz had written about space and time previously, this correspondence is unique for its sustained and detailed account of this aspect of his philosophy. It is also worth pointing out that Leibniz (and after him Kant) continues a long tradition of philosophizing about space and time from the point of view of space, as if the two were always in a strict analogy. It is only rarely that Leibniz deals in any interesting way with time on its own (we shall return to this in section 10).

Newton, and after him Clarke, argued that space and time must be absolute (that is, fixed background constants) and in some sense really existent substances in their own right (at least, this was Leibniz’s reading of Newton). The key argument is often called the “bucket argument.” When an object moves, there must be some way of deciding upon a frame of reference for that motion. With linear motion, the frame does not matter (as far as the mathematics are concerned, it does not matter if the boat is moving away from the shore, or the shore is moving away from the boat); even linear acceleration (changing velocity but not direction) can be accounted for from various frames of reference. However, acceleration in a curve (to take Newton’s example, water forced by the sides of a bucket to swirl in a circle, and thus to rise up the sides of the bucket), could only have one frame of reference. For the water rising against the sides of the bucket can be understood if the water is moving within a stationary universe, but makes no sense if the water is stationary and the universe is spinning. Such curved acceleration requires the postulation of absolute space which makes possible fixed and unique frames of reference. (Similar problems made Einstein’s General Theory of Relativity so much more mathematically complicated than the Special Theory.)

Leibniz, however, has a completely different understanding of space and time. First of all, Leibniz finds the idea that space and time might be substances or substance-like absurd (see, for example, “Correspondence with Clarke,” Leibniz’s Fourth Paper, §8ff). In short, an empty space would be a substance with no properties; it will be a substance that even God cannot modify or destroy.

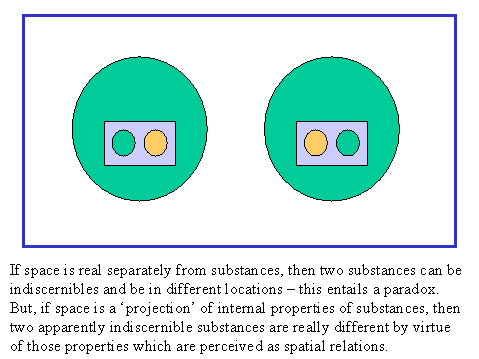
But Leibniz’s most famous arguments for his theory of space and time stem from the principle of sufficient reason (the principle that everything which happens has, at least in principle, an explanation of why it happened as it did and not otherwise). From this principle, together with the law of non-contradiction, Leibniz believes that there follows a third: the principle of the identity of indiscernibles, which states that any entities which are indiscernible with respect to their properties are identical. Leibniz is fond of using leaves as an example. Two leaves often look absolutely identical. But, Leibniz argues, if “two” things are alike in every respect, then they are the same object, and not two things at all. So, it must be the case that no two leaves are ever exactly alike.

Leibniz’s support for the principles of the identity of indiscernibles primarily derives from his commitment to the principle of sufficient reason in the following way. If any objects are in every way the same, but actually distinct, then there would be no sufficient reason (that is, no possible explanation) for why the first is where (and when) it is, and the second is where (and when) it is, and not the other way around. If, then, one posits the possible existence of two identical things (things that differ in number only–that is, one can count them, but that is all), then one also posits the existence of an absurd universe, one in which the principle of sufficient reason is not universally true. Leibniz often expresses this in terms of God: if two things were identical, there would be no sufficient reason for God to choose to put one in the first place and the other in the second place. (Note that Leibniz’s argument relates to a scholastic debate centered on the notion of “Buridan’s Ass.”)

Similar considerations apply to Newtonian absolute space. Leibniz’s argument against the Newton-Clarke position can be understood here as two related reductio ad absurdum arguments. The first concerns the violation of the principle of the identity of indiscernibles. Suppose that space is absolute. Since every region of space would be indiscernible from any other and spatial relations would be construed as extrinsic, it would be possible for two substances to be indiscernible yet distinct in virtue of being in different locations. But this is absurd, Leibniz argues, because it violates the principle of the identity of indiscernibles. Therefore, space must not be absolute (see “Correspondence with Clarke,” Leibniz’s Third Paper). The second reductio concerns the violation of the principle of sufficient reason. Suppose that space is absolute. Leibniz argues that there would then be no sufficient reason for why the whole universe was created here instead of two meters to the left (because no region of space is discernible from any other). Thus, absolute space is absurd, because it violates the principle of sufficient reason (see “Correspondence with Clarke,” Leibniz’s Fourth Paper). (Analogous problems are thought to result from a conception of absolute time.)

b. The Relational Theory

That is the negative portion of Leibniz’s argument. But what does all this say about space? For Leibniz, the location of an object is not a property of an independent space, but a property of the located object itself (and also of every other object relative to it). This means that an object here can indeed be different from an object located elsewhere simply by virtue of its different location, because that location is a real property of it. That is, space and time are internal or intrinsic features of the complete concepts of things, not extrinsic. Let us return to the two identical leaves. All of their properties are the same, except that they are in different locations. But that fact alone makes them completely different substances. To swap them would not just involve moving things in an indifferent space, but would involve changing the things themselves. That is, if the leaf were located elsewhere, it would be a different leaf. A change of location is a change in the object itself, since spatial properties are intrinsic (similarly with location in time).

Leibniz’s view has two major implications. First, there is no absolute location in either space or time; location is always the situation of an object or event relative to other objects and events. Second, space and time are not in themselves real (that is, not substances). Space and time are, rather, ideal. Space and time are just metaphysically illegitimate ways of perceiving certain virtual relations between substances. They are phenomena or, strictly speaking, illusions (although they are illusions that are well-founded upon the internal properties of substances). Thus, illusion and science are fully compatible. For God, who can grasp all at once complete concepts, there is not only no space but also no temptation of an illusion of space. Leibniz uses the analogy of the experience of a building as opposed to its blueprint, its overall design (see, for example, “Correspondence with Arnauld” 12 April 1686 and Monadology §57). It is sometimes convenient to think of space and time as something “out there,” over and above the entities and their relations to each other, but this convenience must not be confused with reality. Space is nothing but the order of co-existent objects; time nothing but the order of successive events. This is usually called a relational theory of space and time. (For more information, see §6 on relative vs. absolute theories of time).

Space and time, according to Leibniz, are thus the hypostatizations of ideal relations, which are real insofar as they symbolize real differences in substances, but illusions to the extent that (i) space or time are taken as a thing in itself, or (ii) spatial/temporal relations are taken to be irreducibly exterior to substances, or (iii) extension or duration are taken to be a real or even fundamental property of substances. Take the analogy of a virtual reality computer program. What one sees on the screen (or in a specially designed virtual reality headset) is the illusion of space and time. Within the computer’s memory are just numbers (and ultimately mere binary information) linked together. These numbers describe in an essentially non-spatial and temporal way a virtual space and time, within which things can “exist,” “move” and “do things.” For example, in the computer’s memory might be stored the number seven, corresponding to a bird. This, in turn, is linked to four further numbers representing three dimensions of space and one of time–that is, the bird’s position. Suppose further the computer contains also the number one, corresponding to the viewer and again linked to four further numbers for the viewer’s position, plus another three giving the direction in which the viewer’s virtual eyes are looking. The bird appears in the viewer’s headset, then, when the fourth number associated with the bird is the same as the viewer’s fourth number (they are together in time), and when the first three numbers of the bird (its position in virtual space) are in a certain algebraic relation to the number representing the viewer’s position and point of view. Space and time are reduced to non-spatial and non-temporal numbers. For Leibniz, God in this analogy apprehends these numbers as numbers, rather than through their translation into space and time.

c. Objections and Replies

This, however, raises a serious logical problem for Leibniz. Recall Leibniz’s theory of truth as the containedness of a predicate in a subject. This seemed acceptable, perhaps, for propositions such as “Caesar crossed the Rubicon” or “Peter is ill.” But what about “This leaf is to the left of that leaf?” The latter proposition involves not one subject, but three (the two leaves, and whatever is occupying the point-of-view from which the one is “to the left”). Leibniz has to argue that all relational predicates are in fact reducible to internal properties of each of the three substances. This includes time, as well as relations such as “the sister of” or “is angry at.” But can all relations be so reduced, at least without radically deforming their sense? Modern logicians often see this as the major flaw in Leibniz’s logic and, by extension, in his metaphysics.

Furthermore, Leibniz must provide a response to the Newtonian bucket argument. Indeed, Leibniz thinks that one simply needs to provide a rule for the reduction of relations. For linear motion the virtual relation is reducible to either or both the object and the universe around it. For non-linear motion, one must posit a rule such that the relation is not symmetrically reducible to either of the subjects (bucket, or universe around it). Rather, non-linear motion is assigned only when, and precisely to the extent that, the one subject shows the effects of the motion. That is, the motion is a property of the water, if the water shows the effects (see “Correspondence with Clarke,” Leibniz’s Fifth Paper, §53). Perhaps it seems strange that the laws of nature should be different for linear as opposed to non-linear motion. It sounds like anarbitrary new law of nature, but Leibniz might respond that it is no more arbitrary that any other law of nature; people have just become used to the illusion of space and time as extrinsic relations of entities that they are not used to thinking in these terms.

Space and time, according to Leibniz, are thus the hypostatizations of ideal relations, which are real insofar as they symbolize real differences in substances, but illusions to the extent that (i) space or time are taken as a thing in itself, or (ii) spatial/temporal relations are taken to be irreducibly exterior to substances, or (iii) extension or duration are taken to be a real or even fundamental property of substances. Take the analogy of a virtual reality computer program. What one sees on the screen (or in a specially designed virtual reality headset) is the illusion of space and time. Within the computer’s memory are just numbers (and ultimately mere binary information) linked together. These numbers describe in an essentially non-spatial and temporal way a virtual space and time, within which things can “exist,” “move” and “do things.” For example, in the computer’s memory might be stored the number seven, corresponding to a bird. This, in turn, is linked to four further numbers representing three dimensions of space and one of time–that is, the bird’s position. Suppose further the computer contains also the number one, corresponding to the viewer and again linked to four further numbers for the viewer’s position, plus another three giving the direction in which the viewer’s virtual eyes are looking. The bird appears in the viewer’s headset, then, when the fourth number associated with the bird is the same as the viewer’s fourth number (they are together in time), and when the first three numbers of the bird (its position in virtual space) are in a certain algebraic relation to the number representing the viewer’s position and point of view. Space and time are reduced to non-spatial and non-temporal numbers. For Leibniz, God in this analogy apprehends these numbers as numbers, rather than through their translation into space and time.

8. Substance as Monad

We are now, finally, ready to get a picture of what Leibniz thinks the universe is really like. It is a strange, and strangely compelling, place. Around the end of the Seventeenth Century, Leibniz famously began to use the word “monad” as his name for substance. “Monad” means that which is one, has no parts and is therefore indivisible. These are the fundamental existing things, according to Leibniz. His theory of monads is meant to be a superior alternative to the theory of atoms that was becoming popular in natural philosophy at the time. Leibniz has many reasons for distinguishing monads from atoms. The easiest to understand is perhaps that while atoms are meant to be the smallest unit of extension out of which all larger extended things are built, monads are non-extended (recall that space is an illusion on Leibniz’s view).

a. Monads and Complete Concepts

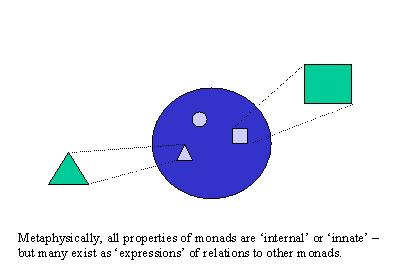
We must begin to understand what a monad is by beginning from the idea of a complete concept. As previously stated, a substance (that is, monad) is that reality which the complete concept represents. A complete concept contains within itself all the predicates of the subject of which it is the concept, and these predicates are related by sufficient reasons into a vast single network of explanation. So, relatedly, the monad must not only exhibit properties, but contain within itself “virtually” or “potentially” all the properties it will exhibit in the future, as well as contain the “trace” of all the properties it did exhibit in the past. In Leibniz’s extraordinary phrase, found frequently in his later work, the monad is “pregnant” with the future and “laden” with the past (see, for example, Monadology §22). All these properties are “folded up” within the monad; they unfold when they have sufficient reason to do so (see, for example, Monadology §61). Furthermore, the network of explanation is indivisible; to divide it would either leave some predicates without a sufficient reason or merely separate two substances that never belonged together in the first place. Correspondingly, the monad is one, simple and indivisible.

Just as in the analysis of space and time Leibniz argues that all relational predicates are actually interior predicates of some complete concept, so the monad’s properties include all of its relations to every other monad in the universe. A monad, then, is self-sufficient. Having all these properties within itself, it doesn’t need to be actually related to or influenced by another other monad. Leibniz writes:

Thus, just like space and time, cause and effect is a “well-founded” illusion. According to Leibniz, causation is to be account for by saying that one thing, A, causes another, B, when the virtual relation between them is more clearly and simply expressed in A than in B. But metaphysically, Leibniz argues, it makes no difference which way around the relation is understood, because the relation itself is not real. Leibniz writes:

Leibniz goes on to insist that the first direction of explanation is much simpler, since the second would involve leaping directly to the action of God to explain the extraordinary action of so many individual bits of water. But that simplicity is hardly the same as truth.

b. Pre-established Harmony, Windowlessness, and Mirroring

So, instead of cause and effect being the basic agency of change, Leibniz is offering a theory of pre-established harmony (sometimes referred to as the hypothesis of concomitance) to understand the apparently inter-related behavior of things. Consider the common analogy of two clocks. The two clocks are on different sides of a room and both keep good time (that is, they tell the same time). Now, someone who didn’t know how clocks work might suspect that one was the master clock and it caused the other clock to always follow it. When two things behave in corresponding ways, then it is often assumed (without any real evidence) that there is causation occurring. But another person who knew about clocks would explain that the two clocks have no influence one on the other, but rather they have a common cause (for example, in the last person to set and wind them). Since then, they have been independently running in sync with one another, not causing each other. On Leibniz’s view, every monad is like a clock, behaving independently of other monads. Nevertheless, every monad is synchronized with one another by God, according to his vast conception of the perfect universe. (We must be careful, however, not to take this mechanical image of a clock too literally. Not all monads are explicable in terms of physical, efficient causes.)

In accordance with his theory of pre-established harmony, Leibniz argues that monads do not affect one another and that each monad expresses the entire universe. He has rather unique and extraordinary set of phrases for this; Leibniz states that every monad mirrors the whole of the universe in that it expresses every other monad, but no monad has a window through which it could actually receive or supply causal influences (see Monadology, §7 & §56). Furthermore, since a monad cannot be influenced, there is no way for a monad to be born or destroyed (except by God through a miracle–defined as something outside the natural course of events). All monads are thus eternal. (It is fair to say that Leibniz’s attempt to account for what happens to “souls” before the birth of body, and after its death, lead him to some colorful, but rather strained, speculations.)

9. Implications of Conceiving Substances as Monads

We will examine briefly four important implications of Leibniz’s account of substance: first, the distinction between metaphysical truth and phenomenal description; second, the idea of little perceptions; third, the infinitely composite nature of all body; and fourth, innate ideas.

a. Levels of Reality

Leibniz posits a distinction between levels or “spheres” in his account of reality (“Discourse on Metaphysics,” §10). The primary, most fundamental level of reality is the metaphysical level, which includes only monads, their perceptions, and their appetitions (no causality, no space, no time–at least as ordinarily understood–each monad spontaneously unfolding according to the kind of thing that it is). The phenomenal or descriptive level involves what appears to be happening from the finite, imperfect perspective of human minds (things cause one another in space and time). Science’s object is the latter, which is an illusion, but in which nothing happens that is not based upon what really happens in the metaphysical level (that is, the illusion is “well-founded”). Therefore, the laws of physics are perfectly correct, as a description. (Berkeley borrows this idea, see especially his “De Motu,” and Kant produces a highly original version of it.) Indeed, Leibniz believes, following Descartes and many other materialists, that all such laws are mechanical in nature, exclusively involving the interaction of momenta and masses–hence his accusation that Newton’s idea of gravity is merely “occult.” However, at the metaphysical level, no account of reality could be less mechanical. Not surprisingly, then, Leibniz’s own contributions to physical science were in the fields of the theory of momentum and engineering.

A serious error would arise only if one took the “objects” of science (matter, motion, space, time, etc.) as if they were real in themselves. Consider the following analogy: in monitoring a nation’s economy, it is sometimes convenient to speak of a retail price index, which is a way of keeping track of the average change in the prices of millions of items. But there is nothing for sale anywhere which costs just that amount. As a measure it works well, provided one does not take it literally. Science, in order to be possible for finite minds, involves that kind of simplification or “abbreviation” (see, for example, “Letter to Arnauld,” 30 April 1687).

b. Little Perceptions

Leibniz is one of the first philosophers to have analyzed the importance of that which is “unconscious” in one’s mental life. That a monad is a “mirror” of the whole universe entails that one’s soul will actually have an infinite number and complexity of perceptions. Obviously, however, one does not apperceive (that is, one is not conscious of) all these little perceptions, as Leibniz calls them. Thus, perception for Leibniz does not mean apperception. (Leibniz argues that this is a major error on Descartes’ part.) Further, where one is conscious of some perception, it will be of a blurred composite perception. Leibniz’s analogy is of the roar of the waves of the beach: the seemingly singular sound of which one is conscious is in fact made up of a vast number of individual sounds of which one is not conscious–droplets of water smacking into one another.

For Leibniz, little perceptions are an important philosophical insight. First and foremost, this relates to one of Leibniz’s main general principles, the principle of continuity. Nature, Leibniz claims, “never makes leaps” (New Essays on Human Understanding, 56). This follows, Leibniz believes, from the principle of sufficient reason together with the idea of the perfection of the universe (consisting of something like plenitude). But the idea of little perceptions allows Leibniz to account for how such continuity actually happens even in everyday circumstances. The principle of continuity is very important for Leibniz’s physics (see “Specimen Dynamicum”) and turns up in Leibniz’s account of change in the monad (see below).

Second, little perceptions explain the acquisition of innumerable minor habits and customs, which make up a huge part of one’s distinctiveness as an individual personality. Such habits accumulate continuously and gradually, rather than all at once like decisions, and thus completely bypass the conscious will. Further, these little perceptions account for one’s pre-conscious connection with the world. For Leibniz, one’s relation with the world is not one just of knowledge, or of apperceived sensation. An individual’s relation with the world is richer than either of these, a kind of background feeling of being-a-part-of. (Thus, a thorough-going skepticism, however plausible at a logical level, is ultimately absurd.)

Finally, Leibniz’s idea of little perceptions gives a phenomenal (rather than metaphysical) account for the impossibility of real indiscernibles: there will always be differences in the petite perceptions of otherwise very similar monads. The differences may not be observable at the moment, but will “unfold in the fullness of time” into a discernible difference (New Essays on Human Understanding, 245-6).

c. Composites and Substantial Forms

According to Leibniz, everything one perceives which is a unified being must be a single monad. Everything else is a composite of many monads. A coffee cup, for example, is made of many monads (an infinite number, actually). In everyday life, one tends to call it a single thing only because the monads all act together. One’s soul, however, and the soul of every other living thing, is a single monad which “controls” a composite body. Leibniz thus says that, at least for living things, one must posit substantial forms, as the principle of the unity of certain living composites. (See, for example, “A New System of Nature.” The term is derived from Aristotle: that which structures and governs the changes of mere matter in order to make a thing what it is.) One’s soul, a monad otherwise like any other monad, thus becomes the substantial form of one’s otherwise merely aggregate body.

Furthermore, according to Leibniz, such composite bodies must be made of an infinite number of other inanimate as well as animated monads. This follows from the universe being the most perfect possible, which, again, seems to mean the richest in controlled complexity, in “plenitude.” Leibniz argues that it would be a great waste of possible perfection to only allow living beings to have bodies at that particular level of aggregation with which one is phenomenally familiar. (Perhaps Leibniz was understandably impressed by the different levels of magnitude being revealed by relatively recently invented instruments like the microscope and telescope.) Leibniz writes:

(Note: Although there is an extraordinary sublimity of such an image, Leibniz is often accused of making rather too much of an inadequate conception of the infinite.)

Further, the particular monads making up one’s body are constantly changing as one breaths in and out, sheds skin, etc., although not all at once. The substantial form is thus a unified explanation of bodily form and function. A mere chunk of stuff has, of course, an explanation, but not a unified one–not in one monad, the soul. Leibniz thus distinguishes four types of monads: humans, animals, plants, and matter. All have perceptions, in the sense that they have internal properties that “express” external relations; the first three have substantial forms, and thus appetition; the first two have memory; but only the first has reason (see Monadology §§18-19 & 29).

d. Innate Ideas

An innate idea is any idea which is intrinsic to the mind rather than arriving in some way from outside it. During this period in philosophy, innate ideas tended to be opposed to the thorough - going empiricism of Locke. Like Descartes before him–and for many of the same reasons – Leibniz found it necessary to posit the existence of innate ideas. At the metaphysical level, since monads have no “windows,” it must be the case that all ideas are innate. That is to say, an idea in one’s monad/soul is just another property of that monad, which happens according to an entirely internal explanation represented by the complete concept. But at the phenomenal level, it is certainly the case that many ideas are represented as arriving through one’s senses. In general, at least any relation in space or time will appear in this way.

Thus, one could imagine Leibniz being a thorough - going empiricist at the phenomenal level of description. This would amount to the claim that the metaphysically true innateness of all ideas is epistemologically useless information. Leibniz finds it necessary, therefore, to advance the following arguments in favor of phenomenally innate ideas:

1. Some ideas are characterized by universal necessity, such as ideas in geometry, logic, metaphysics, morality, and theology. But it is impossible to derive universal necessity from experience. (Note that this argument is hardly new to Leibniz.)
2. An innate idea need not be an idea consciously possessed (because of “little perceptions,” for example). An innate idea can be potential, as an inclination of reason, as a rigid distortion in Locke’ stabula rasa. (Here, Leibniz provides the famous analogy of the veins in the marble prior to the sculptor’s work.) It requires “attention” (especially in the form of philosophical thinking) to bring to explicit consciousness the operation, and to clarify the content, of these innate ideas.
3. Consider the possibility of foreseeing an event that is not similar to (and thus merely an associated repetition of) a past event. By using rational principles of physics, for example, one can analyze a situation and predict the outcome of all the masses and forces, even without ever having experienced a similar situation or outcome. This, Leibniz says, is the privilege of humans over animals (“brutes”), who only have the “shadow” of reason, because they can only move from one idea to another by association of similars (see Leibniz’s joke about empiricists in Monadology, §28).

Thus, at the phenomenal level, Leibniz can distinguish between innate and empirical ideas. An empirical idea is a property of a monad which itself expresses a relation to some other substance or which arises from another internal property that is the expression of an external substance. Although the difference between empirical and innate is in fact an illusion, it does make a difference, for example, to the methodology of the sciences. This is similar to the distinction made above between the idea of truth (as the containedness of the predicate in the subject), and the pragmatic/methodological issue of how one comes to know that truth. The latter is not irrelevant, except to the foundation and definition of truth. (Leibniz’s most extensive discussion of innate ideas, not surprisingly, is in the New Essays on Human Understanding.)

10. Monadic Activity and Time

Correlate to the inter-connectedness of predicates in the complete concept is an active power in the monad, which thus always acts out its predicates spontaneously. Predicates are, to use a fascinating metaphor of Leibniz’s, “folded up” within the monad. In later writings such as the Monadology, Leibniz describes this using the Aristotelian/Medieval idea of entelechy: the becoming actual or achievement of a potential. This word is derived from the idea of perfections. What becomes actual strives to finish or perfect the potential, to realize the complete concept, to unfold itself perfectly as what it is in its entirety. This active power is the essence of the monad. Leibniz has several different names for this property (or closely related properties) of monads: entelechy, active power, conatus or nisus (effort/striving, or urge/desire), primary force, internal principle of change, and even light (in “On the Principle of Indiscernibles”).

This activity is not just a property of human souls, but of all types of monads. This inner activity must mean not only being the source of action, but also being affected (passivity), and of resisting (inertia). Again, what one calls “passivity” is just a more complex and subtle form of activity. Both a monad’s activity and resistance, of course, follow from its complete concept, and are expressed in phenomena as causes and as effects. Change in a monad is the intelligible, constantly, and continuously (recalling here the principle of continuity discussed above) unfolding being of a thing, from itself, to itself. “Intelligible” here means: (i) according to sufficient reason, not random or chaotic; and (ii) acting as if designed or purposed, as if alive – hence Leibniz’s contribution to the philosophical tradition of “vitalism.”

It is important to understand that this is not just a power to act, conceived as separable from the action and its result. Rather, Leibniz insists that one must understand that power together with (i) the sufficient reason of that power; (ii) the determination of the action at a certain time and in a certain way; (iii) together with all the results of the action, first as the merely potential and then as the actual. (See “On the Principle of Indiscernibles,” and Monadology §§11-15.) One is not, therefore, to understand it as a sequence of states, the individual bits of which are even ideally separable (except as an object of mere description for science), nor a sequence of causes and effects, again understood to be ideally separable (as if there could have been the cause without the effect). All this follows from the complete concept, the predicates of which are connected in one concept. Each state therefore contains the definite trace of all the past, and is (in Leibniz’s famous phrase) “pregnant” with the future.

But time, like space, is an illusion. How then is one to understand change without time? The important question is: what conception of time is being discussed? Just like space, Leibniz is objecting to any conception of time which is exterior to the objects that are normally said to be “in” time (time as an exterior framework, a dimension). Also, he objects to time as mere chronology, a conception of time as a sequence of “now points” that are ideally separable from one another (that is, not essentially continuous) and are countable and orderable separately from any thing being “in” them (that is, abstract).

However, in discussing relational properties above (and, in particular, Leibniz’s response to the Newton-Clarke argument about non-linear motion), “space” was in a sense preserved as a set of rules about the representative properties of monads. Here, too, but in a more profound way, “time” is preserved immanently to the monad. The active principle of change discussed above is immanent to monads, and no one state can be separated from all the others, without completely altering the thing in question into a thing that never changes (that has only the one state for all eternity). For Leibniz, the past and future are no more disconnected, in fact less, from the present than “here” is from “there.” Both distinctions are illusions, but temporal relations in a substance form an explanatory, intelligible sequence of a self-same thing. The principle of change becomes an original, internal and active power of the thing constantly becoming the thing that it is, as the spontaneous happening and internal principle of the particular order of things which make up that substance. In other words, substances unfold, become the things God always knew them to be, in a time that is nothing other than precisely that becoming.

Time, then, has three levels, according to Leibniz

1. the atemporality or eternality of God;
2. the continuous immanent becoming-itself of the monad as entelechy;
3. time as the external framework of a chronology of “nows.”

The difference between (ii) and (iii) is made clear by the account of the internal principle of change. The real difference between the necessary being of God and the contingent, created finitude of a human being is the difference between (i) and (ii).

11. Influence

Leibniz’s mathematics, in parallel to Newton’s, made a significant difference in European science of the 18th century. Other than that, however, his contributions as engineer or logician were relatively quickly forgotten and had to later be re-invented elsewhere.

However, Leibniz’s metaphysics was highly influential, renewing the Cartesian project of rational metaphysics, and bequeathing a set of problems and approaches that had a huge impact on much of 18th century philosophy. Kant above all would have been unthinkable without Leibniz’s philosophy, especially the accounts of space and time, of sufficient reason, of the distinction between phenomenal and metaphysical reality, and his approach to the problem of freedom. Rarely did Kant agree with his great predecessor–indeed, rendering the whole Cartesian/Leibnizian approach conceptually impossible–but the influence was nevertheless necessary. After Kant, Leibniz was more often than not a mine of individual fascinating ideas, rather than a systematic philosopher, ideas appearing (in greatly modified forms) in for example Hegelian idealism, romanticism, and Bergson.

In the 20th century, Leibniz has been widely studied by Anglo-American “analytic” philosophy as a great logician who made significant contributions to, for example, the theory of identity and modal logic. In Continental European philosophy, Leibniz has perhaps been less commonly treated as a great predecessor, although fascinating texts by Heidegger and, much later, by Deleuze, show the continuing fertility of his philosophical ideas.

12. Editions of Leibniz

As noted above, Leibniz did not publish much in his lifetime which fits the familiar description of a philosophy book. Much was published, however, shortly after his death. But there remained for the dedication of future editors a huge estate of short papers, letters, drafts of letters, and notes. The standard edition of the works of Leibniz is the Akademie-Verlag of Berlin. The most comprehensive collection of these in English, together with some published material, is in Leibniz, Philosophical Papers and Letters, translated and edited by L. E. Loemker, 2 volumes, University of Chicago Press, 1956.

Several good, inexpensive and shorter anthologies of key texts:

• Philosophical Essays. Edited and translated by Ariew and Garber. Hackett, 1989.
• Philosophical Texts. Translated by Francks and Woolhouse. Oxford University Press, 1998.
• Philosophical Writings. Edited by Parkinson, translated by Morris and Parkinson. Everyman, 1973.

Finally, editions in English of more specialized selections, the longer texts, and correspondences of Leibniz:

• The Correspondence with Clarke. Edited by Alexander. Manchester University Press, 1956.
• The Leibniz-Arnauld Correspondence. Edited and translated by Mason. Manchester University Press, 1967.
• Logical Papers. Edited and translated by Parkinson. Oxford University Press, 1966.
• The Political Writings of Leibniz. Edited and translated by Riley. Cambridge University Press, 1972.
• New Essays on Human Understanding. Edited and translated by Remnant and Bennett. Cambridge University Press, 1996.
• Theodicy. Edited by Farrer, translated by Huggard. Routledge and Kegan Paul, 1951.

Author Information

Douglas Burnham
Email: H.D.Burnham@staffs.ac.uk
Staffordshire University
United Kingdom

Tags: Philosophy, Metaphysics, Logic

Access and use of this site by any means implies consent to the Agreement of Use. © Hellene Sun